Un numero speciale, il numero aureo. Anche se si potrebbe pensare che la matematica non c’entra niente con la realtà del mondo, la matematica è il linguaggio della natura. Lo stesso Galileo Galilei affermò che l’universo è come un grandissimo libro scritto in lingua matematica, e per leggerlo, prima è necessario conoscere il linguaggio.
“In qualità di Affiliato Amazon io ricevo un guadagno dagli acquisti idonei”
NUMERO AUREO
C’è un numero ad esempio che è davvero speciale. Si chiama Phi – Φ (si legge “fi”) o numero aureo, ed è un numero irrazionale (che non termina mai) che equivale circa a 1,6180339887 ecc…
Per comodità si fa coincidere a tale numero il valore di 1,618. Il numero Phi è una costante che corrisponde al rapporto fra due lunghezze disuguali dove la maggiore di queste è medio proporzionale tra la minore b e la somma delle due (a + b). O meglio, esso esprime il rapporto tra due grandezze dove la somma delle due sta alla più grande, come la più grande sta alla più piccola. (a+b):a=a:b
La sezione aurea è una rappresentazione figurativa del numero aureo.
PERCHÉ’ IL NUMERO AUREO E’ IMPORTANTE?
E’ talmente importante che alcuni dei suoi soprannomi sono “Il numero di Dio” o “l’impronta digitale di Dio”. Per secoli la sezione aurea ha rappresentato la prova di un legame invisibile tra macrocosmo e microcosmo, tra Dio e l’uomo, tra il tutto e la parte, come se la parte più grande si ripetesse all’infinito attraverso infinite suddivisioni.
DOVE SI TROVA IL NUMERO AUREO?
Si trova in tantissimi elementi naturali e anche in molte opere d’arte.
In natura molti elementi riprendono la rappresentazione del numero aureo: la conchiglia del mollusco Nautilus, la struttura delle galassie, le corna a spirale di molti mammiferi, la struttura a doppia elica del DNA, la forma degli uragani, le proporzioni delle ossa negli animali e molti altri.
LA SCOPERTA DEL NUMERO AUREO
Non si è certi se i popoli antichi prima dei Greci conoscessero la sezione aurea e la utilizzassero consapevolmente nelle loro opere. Ad esempio Babilonesi ed Egizi.
Alcune tavolette riportanti calcoli computazionali testimoniano conoscenze sia matematiche sia geometriche dei Babilonesi, tali da poter ottenere buone approssimazioni dell’area del pentagono e perfino del pi greco.
Agli antichi Egizi spesso sono state attribuite conoscenze matematiche molto avanzate. Nella Piramide di Cheope nella piana di Giza è stato riscontrata la presenza della sezione aurea.
La definizione del rapporto aureo venne fissata attorno al VI secolo a.C., per opera della scuola pitagorica (i discepoli e seguaci di Pitagora), nell’Italia meridionale. Associarono ad esso il concetto di incommensurabilità.
Il Partenone di Atene presenta una facciata perfettamente inscrivibile nelle proporzioni di un rettangolo aureo (ossia un rettangolo costruito in base alle “regole” della sezione aurea).
Arte gotica
Nel 1919 Frederik Macody Lund, uno storico studioso delle strutture gotiche, arrivò alla conclusione che la Cattedrale di Chartres (iniziata nel 12° secolo), Notre-Dame di Laon (1157-1205) e Notre Dame de Paris (1160) fossero state progettate secondo il rapporto aureo.
La divina proporzione nel Medioevo era utilizzata in modo consapevole poiché questo fatto è stato spesso documentato dagli autori.
Il pentagono regolare, il pentagono stellato o il rettangolo aureo appaiono come schemi di base per sculture o interi edifici come si può vedere anche nella facciata gotica dell’Università di Salamanca in Spagna.
Altri studiosi sostengono, invece, che fino alla pubblicazione del libro “De divina proportione” di Luca Pacioli (nel 1509), la sezione aurea era sconosciuta ad artisti e architetti che comunque la utilizzavano inconsapevolmente.
Oltre agli archi di trionfo della Roma classica si rifanno alla proporzione aurea anche altre civiltà’ molto diverse. Non lontano dal lago Titicaca, vicino a La Paz, attuale capitale della Bolivia, troviamo la Porta del Sole, un monumento di una cultura preincaica risalente al 1500 a.C., interamente proporzionato in base al phi.
Il Taj Mahal nell’India settentrionale è un mausoleo costruito nel 1632 dall’imperatore Moghul Shah Jahan in memoria della moglie. Si pensa che l’architetto sia stato Ustad Ahmad Lahauri. La sua struttura risulta inserita e modulata dai rapporti della sezione aurea.
Il Rinascimento
Il rapporto aureo fu largamente usato anche nel Rinascimento.
Artisti e matematici del rinascimento si interessarono molto alla matematica e specificatamente alla sezione aurea. Tra loro soprattutto Leon Battista Alberti, Piero della Francesca, Leonardo da Vinci.
Per fare degli esempi, le dimensioni della Monnalisa di Leonardo da Vinci sono in rapporto aureo. La composizione di opere come L’ultima cena si basa sul rettangolo aureo che si ritrova in molte parti dell’opera.
A Venezia nel 1509 viene pubblicato il libro De divina proportione di Luca Pacioli, in cui si divulgava l’esistenza del numero aureo che viene chiamato proporzione divina.
Architettura moderna
Nell’Ottocento la sezione aurea si diffonde consapevolmente nel campo dell’arte per la convinzione che essa costituisse un canone estetico “naturale”, per la sua ricorrenza in natura. Si riteneva che le sue proporzioni conferissero uno straordinario senso di armonia alle opere d’arte.
In tempi più recenti, il Palazzo di Vetro delle Nazione Unite ha proporzioni auree, come pure la monumentale rampa del Museo Guggenheim di New York a forma di Nautilus, ovvero di spirale.
SUCCESSIONE FIBONACCI
Nel 1202 Leonardo Fibonacci pubblica il suo Liber abaci, il libro col quale si diffonderanno in Europa le cifre indo-arabe, semplificando le modalità di calcolo nelle operazioni quotidiane.
Nel medesimo libro, Fibonacci introdusse pure per la prima volta, involontariamente, il concetto di successione ricorsiva, che porta il suo nome. Nella successione di Fibonacci ogni termine è la somma dei due precedenti.
Si parte da 0 e 1; poi da lì si inizia a sommare: 0+1 fa 1, dunque nella successione a 0 e 1 aggiungeremo un 1. Poi 1+1 fa due, quindi si aggiunge un 2
1,1,2,3,5,8,13,21,34,55,89,144,233,377… e così via.
Relazione tra numero aureo e la serie di Fibonacci
Nel 1611 Keplero scoprì la relazione tra il numero aureo e la serie di Fibonacci.
Dividendo ogni numero per il suo precedente si ottiene un valore che approssima quello di Phi (1,618…). Più si sale nella sequenza più l’approssimazione si avvicina al valore di Phi.
“In qualità di Affiliato Amazon io ricevo un guadagno dagli acquisti idonei”
SPIRALE LOGARITMICA
La spirale logaritmica è una figura geometrica ottenuta, come scoprì per la prima volta Cartesio, considerando la traiettoria di un punto che si muove di moto uniformemente accelerato su una semiretta, la quale ruota uniformemente intorno alla sua origine.
La spirale logaritmica è definita proporzionale. Ogni raggio vettore sarà più ampio del precedente secondo un rapporto costante, facendo sì che la curva, crescendo, non cambi forma. In particolare, le distanze tra i bracci della spirale aumentano secondo una progressione geometrica.
Allontanandosi sempre di più dall’origine, aumentano le dimensioni della spirale, ma essa è sempre somigliante a se stessa.
Una spirale logaritmica in cui il rapporto costante tra i raggi consecutivi è pari a φ si dice aurea.
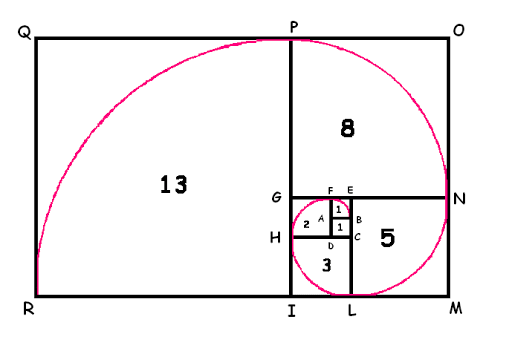
Creando progressivi quadrati con lato uguale ai numeri della serie di Fibonacci, si ottengono “rettangoli aurei”, il cui lato maggiore è diviso secondo la proporzione aurea. Se intersechiamo con una curva gli angoli opposti di ciascun quadrato, otteniamo la famosa spirale aurea.
Questa si ritrova in natura in infinite varianti, dal moto delle particelle atomiche a quello delle galassie. La coda del cavalluccio marino segue una perfetta spirale logaritmica.
Il cavolo romano presenta una crescita frattale delle sue infiorescenze secondo una spirale logaritmica.
I semi di girasole crescono lungo due serie contrapposte di spirali logaritmiche. Il numero delle spirali, in senso orario e in senso antiorario, dipende dalle dimensioni del fiore ed è correlato alla successione di Fibonacci.
I falchi si avvicinano alla loro preda secondo una spirale logaritmica.
La conchiglia del Nautilus è forse il più bell’esempio di spirale aurea in natura.
SEZIONE AUREA E PENTAGONO
La diagonale ed il lato del Pentagono hanno come rapporto proprio phi.
In un triangolo isoscele con gli angoli alla base pari a 72° il lato e la base hanno come rapporto phi. Si dice allora che il triangolo è aureo.
Ogni pentagono contiene un pentagramma, ovvero la stella a cinque punte che si ottiene collegando tutti i vertici del pentagono tramite diagonali. La forma del pentagramma è riscontrabile molto spesso in natura.
La sezione aurea e i frattali
La sezione aurea e la successione di Fibonacci ci sono utili per comprendere la geometria frattale, di cui parleremo nel prossimo articolo.
Fonti:Wikipedia
Foto di Annette Meyer da Pixabay